0:00
みなさんこんにちは。
人工知能ラボの助手です。
前回は、回帰分析を行う上で大事な3ステップのうち、
ステップ①について簡単に説明しました。
今回は引き続き、ステップ②について学んでいきましょう。
②パラメータを評価する基準を設定
では、関数の関係を推測するという本来の目的において
「何をもって推測できたとするか」というゴールを設定する
ステップとなります。
もう少し具体的にいうと、
ステップ①で仮定したモデルに含まれるパラメータが
どのような状態のときに得られたデータにうまくフィットし、
関数の関係を推測できたといえるか、を設定するということになります。
それでは、ステップ①の内容と合わせながら具体的に考えてみましょう。
前回説明した、最も単純なモデルは
y=ax+b の形で表されると説明しました。
この式でのパラメータは「a」と「b」です。
この2つのパラメータが決まれば、関数が決まるというわけです。
例えば、
a=2、b=1 なら y=2x+1
a=-4、b=7 なら y=-4x+7
というように関数が決まるわけです。
実際の回帰分析の流れに沿って考えてみます。
例えば、
(x,y) = (1,3) 、 (2,9)
という2つのデータが得られたとしましょう。
このとき、この2つの点を通る(つまりデータにフィットする)ような
関数を推測するというような場合、みなさんならどのように
考えるでしょうか。
学校の授業でやったような問題ですね。
この場合、 y=ax+b の x と y に(1,3) と (2,9) を代入して、
aとbについての方程式を解くことで関数がわかりますね。
ちなみに、この2点を通る関数は y=6x-3
つまり、パラメータはそれぞれ a=6、b=-3
ということになります。
このように、簡単な例であれば関数を決定することはできるのです。
この関数で、「x=3 のときyはどのような値をとるか」を考えたい場合
関数のxに3を代入して、y=… の形にすれば
これはつまり、yの値を予測できたことになります。
それでは、得られたデータがもっと多く、
モデルがy=ax+bのように簡単でない場合
このようにパラメータを決定することができるでしょうか。
答えはNOです。
そこで必要となるのが、ステップ②となるわけなのです。
まず、回帰分析を行う上で、関数がすべてのデータにフィットする
といったことはあまり考えられません。
もちろん、すべてのデータにフィットするよう
モデルを決定すればできなくはないのですが、
それだと良い回帰分析とは言えないことがほとんどであり、
このような状態を「過学習」と呼びます。
この過学習については、いずれ別の機会に説明しますね。
では、すべてのデータにフィットしないとは
どのような状態なのでしょうか。
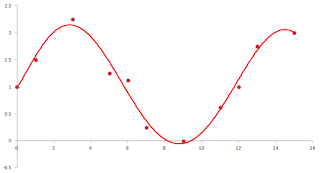
それは、得られたデータと推測した関数との間に誤差がある、
ということなのです。
冒頭の画像は、まさにその状態を表しているのです。
逆に、すべてのデータをフィットさせた場合、
予測した関数はぐにゃぐにゃになってしまい
「きれいに予測した!」
とは直感的にも言えなさそうですね。
次回は、ステップ② 後半、
誤差がある場合を考えて、パラメータを決定できるようになりましょう!