0:00
みなさんこんにちは。
人工知能ラボの助手です。
前回は博士が回帰分析を行う上で大事な、
3つのステップを説明してくれましたね。
今回はその3つのステップの1つ目について
話していきたいと思います。
①パラメータを含む数式モデルを仮定
とは、得られたデータをみて、
「このデータはどのような数式で表わされるのだろうか」
ということを予測するということです。
考えるモデルとしては色々ありますが、
もっとも単純なものだと、 y=ax+b の形で
表わす線形回帰(単回帰)ですね。
ここに、axの項を増やしていくと重回帰になります。
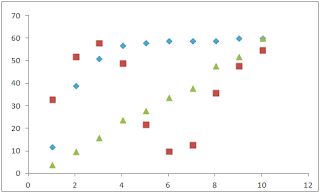
用途別に考えてみると、画像の青のデータ
のような、上昇しつつも収束していくような
場合には対数関数、赤のデータのように周期性
が表れているときにはsin、cosなどの三角関数
が適しています。
このモデルを適切に仮定できるかで、回帰の
結果の良し悪しが決まってくるとても大切なステップです。
とはいっても、得られたデータだけから
「そのデータがどのような形の数式で表わせるのか」
ということを推測するのは、よっぽどデータの規則性
が単純でなければ難しいことです。
なので、基本的にはいろんなモデルを試していって、
上手くフィットする数式モデルを決定していくという
試行錯誤になります。
このモデルを適切に決めるというのも、経験によって
培われていくスキルなのかもしれませんね。
それでは次回は、
②パラメータを評価する基準を決定
について学んでいきましょう。
人工知能ラボの助手です。
前回は博士が回帰分析を行う上で大事な、
3つのステップを説明してくれましたね。
今回はその3つのステップの1つ目について
話していきたいと思います。
①パラメータを含む数式モデルを仮定
とは、得られたデータをみて、
「このデータはどのような数式で表わされるのだろうか」
ということを予測するということです。
考えるモデルとしては色々ありますが、
もっとも単純なものだと、 y=ax+b の形で
表わす線形回帰(単回帰)ですね。
ここに、axの項を増やしていくと重回帰になります。
用途別に考えてみると、画像の青のデータ
のような、上昇しつつも収束していくような
場合には対数関数、赤のデータのように周期性
が表れているときにはsin、cosなどの三角関数
が適しています。
このモデルを適切に仮定できるかで、回帰の
結果の良し悪しが決まってくるとても大切なステップです。
とはいっても、得られたデータだけから
「そのデータがどのような形の数式で表わせるのか」
ということを推測するのは、よっぽどデータの規則性
が単純でなければ難しいことです。
なので、基本的にはいろんなモデルを試していって、
上手くフィットする数式モデルを決定していくという
試行錯誤になります。
このモデルを適切に決めるというのも、経験によって
培われていくスキルなのかもしれませんね。
それでは次回は、
②パラメータを評価する基準を決定
について学んでいきましょう。