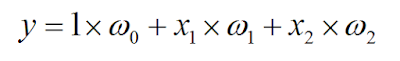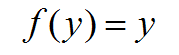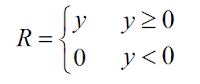0:00
みなさんこんにちは。
人工知能ラボの助手です。
今回からは、機械学習の中でも花形、
ニューラルネットワークの基礎、
パーセプトロンについて
説明をしていきます。
パーセプトロンというモデルは、
そもそも動物の神経細胞(ニューロン)をもとに発明されました。
これは、他の細胞から複数の入力を受け取り、
入力が一定以上の値以上に達すると、
信号を出力する(発火)というモデルです。
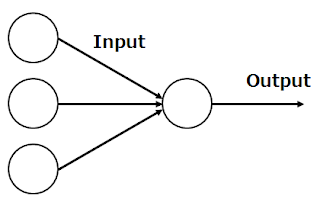
この記事のトップ画像はその模式図です。
この絵では3つの入力から1つの出力をするモデルですが、
実際にはいくつであっても問題はありません。
それでは、実際に式を追って
確認してみましょう。
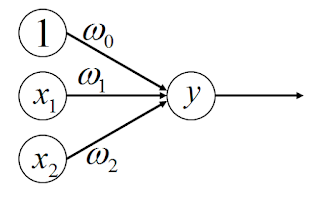
今回は、上図のようなモデルを考えましょう。
まず、入力ノードから出力ノードに向かっている矢印は、
出力に対するそれぞれの入力ノードからの重みです。
例えば、1番目の入力ノードの値は10倍して、
2番目の入力ノードの値は0.1倍する…
のように、重みをかけることになります。
ですので、出力ノードの値は次のようになるはずですね。
という構造です。
ここでよく考えられるのが、
「ある一定の数値hを超えたら発火して、
超えなかったら出力を0にしたい」
という構造です。
この構造のモデルはよく機械学習で用いられるモデルです。
先程の式では、発火する場合のことのみ考えていましたので
発火しない場合を含めて挙げる必要があります。
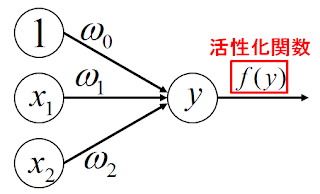
そこで用いるのが活性化関数というものです。
活性化関数とは、出力ノードの値によって、
実際の出力値を決めている関数のことです。
次の図は、活性化関数を改めて考慮したモデルです。
最もシンプルな活性化関数は、
出力ノードの値をそのまま出力する関数となるので、
ですね。
今回の場合、一定の値h(このような値のことをしきい値と言います)
を超えた場合に出力、
超えなかったら0というような活性化関数は
“ランプ関数”
と呼ばれます。
このランプ関数Rは次のように表せます。
これを用いることで今回のモデルは
次のように書きかえることで表せます。
カッコ内は、入力された値と各重みの和より、
しきい値が高ければ正、低ければ負(0未満)となるため、
先程のランプ関数の定義の通り、出力ノードの値が正の時のみ
値を出力するというモデルとなりました。
次回の記事では、もう少しパーセプトロンの特徴と、
それを用いた分類までを説明します。
それでは、今回はこの辺で。
お疲れさまでした！